Circle packing in a square

Circle packing in a square is a packing problem in recreational mathematics, where the aim is to pack n unit circles into the smallest possible square; or, equivalently, to arrange n points in a unit square for the greatest minimal separation, d_n, between points.^[1] To convert between these two formulations of the problem, the square side for unit circles will be 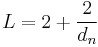$L=2%2B\frac{2}{d_n}$ .

Optimal solutions have been proven for N≤30. Solutions up to N=20 are shown below.^[2]:

Number of circles	Square size	d_n^[1]
1	2
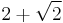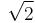2	$2%2B\sqrt{2}$ ≈ 3.414...	$\sqrt{2}$ ≈ 1.414...
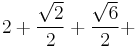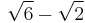3	$2%2B\frac{\sqrt{2}}{2}%2B\frac{\sqrt{6}}{2}%2B$ ≈ 3.931...	$\sqrt{6} - \sqrt{2}$ ≈ 1.035...
4	4	1
5	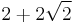$2%2B2\sqrt{2}$ ≈ 4.828...	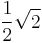$\frac{1}{2} \sqrt{2}$ ≈ 0.707...
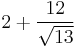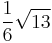6	$2 %2B \frac{12}{\sqrt{13}}$ ≈ 5.328...	$\frac{1}{6} \sqrt{13}$ ≈ 0.601...
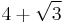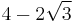7	$4%2B \sqrt{3}$ ≈ 5.732...	$4- 2\sqrt{3}$ ≈ 0.536...
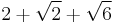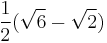8	$2 %2B \sqrt{2} %2B \sqrt{6}$ ≈ 5.863...	$\frac{1}{2}(\sqrt{6} - \sqrt{2})$ ≈ 0.518...
9	6	0.5
10	6.747...	0.421...
11	7.022...	0.398...
12	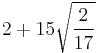$2 %2B 15\sqrt{\frac{2}{17}}$ ≈ 7.144...	0.389...
13	7.463...	0.366...
14	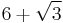$6 %2B \sqrt{3}$ ≈ 7.732...	0.348...
15	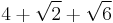$4 %2B \sqrt{2} %2B \sqrt{6}$ ≈ 7.863...	0.341...
16	8	0.333...
17	8.532...	0.306...
18	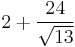$2 %2B \frac{24}{\sqrt{13}}$ ≈ 8.656...	0.300...
19	8.907...	0.290...
20	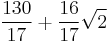$\frac{130}{17} %2B \frac{16}{17} \sqrt{2}$ ≈ 8.978...	0.287...

References

^ ^a ^b Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991). Unsolved Problems in Geometry. New York: Springer-Verlag. pp. 108–110. ISBN 0-387-97506-3.
^ Eckard Specht (20 May 2010). "The best known packings of equal circles in a square". http://hydra.nat.uni-magdeburg.de/packing/csq/csq.html. Retrieved 25 May 2010.